[컴퓨터구조]데이터의 표현 정리
류명운
·2015. 10. 9. 20:14
3장 데이터의 표현
수의 표현
- 10진법: 0에서 9까지의 10개의 기호를 사용한 수치 표현 방법
- 2진법: false가 올라가 있는 상태를 '1'로 나타내고 내려가 있는 상태를 '0'으로 나타내는 2진법의 수의 체계
- 8진법: ex) 124(8) = (1*8^2) + (2x8^1) + (4*8^0) = 64 + 16 + 4 = 82(10)으로 표현
- 16진법: ex) ABC(16) = (10*16^2) + (11*16^1) + (12*16^0) = 2560 + 176 + 12 = 2748(10)
소수의 표현
2진수의 소수 표현
|
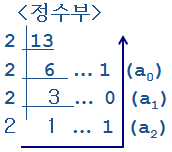
(Quiz1) 10진수 13.75를 2진수로 표현하시오 -> 13(10) = 1101(2), 0.75(10) = 0.11(2) -> 13.75(10) = 1101.11(2)
(Quiz2) 다음 수들을 10진수로 변환하라 1) 2FA(16진수) -> (2*16^2) + (15*16^1) + (10*16^0) -> 512+240+10=762(10) 2) 5432.1(8진수) -> (5*8^3) + (4*8^2) + (3*8^1) + (2*8^0) + (1*8^-1) = (512 + 254 + 24 + 2) + 0.125 -> 792.125 3) 101010.01(2진수) -> 42.25(10)
(Quiz3) 1010.101(2)를 십진수로 변환하라 -> 1010(2) = 10(10) / 0.101(2) = (1*2^-1) + (1*2^-3) = (1/2) + (1/8) = (5/8) = 0.625(10) -> 10 + 0.625 = 10.625(10)
(Quiz4) 십진수 23과 0.625를 각각 진수로 변환하라 -> 23(10) = 10111(2) / 0.625(10) = 0.101(2) -> 10111.101(2)
(Quiz5) 517.390625(10) 값을 8진수로 변환하시오 -> 정수부와 소수부를 분리함 :527 / 390625 ->@ (정부수는 몫이 0이 될때까지 n진수로 나누어야함, 답은 나머지 오름차순) -> 527/8 = 65(나머지 7) -> 65/8 = 8(나머지 1) -> 8/8 = 1(나머지 0) -> 1/8 = 0(몫이 0, 나머지1) -> 나머지를 오름차순하면 정수부의 값은 1017(8) ->@ (소수부는 소수부가 0이 될때까지 n진수로 곱해야함, 답은 소수부 내림차순) -> 0.390625*8 = 3.125(정수부 3) -> 0.125*8 = 1.0(소수부 0, 정수부 1) -> 0.31(8) ->(최종답)1017.31(8) |
보수
: 음의 정수를 나타내기 위해 보수의 표현을 사용함
: 2진수에는 1의 보수와 2의 보수 표현
1의 보수: '1'과 '0'의 값을 바꿔 주면 됨
ex) 10101010 -> 01010101
2의 보수: 1의 보수를 취해주고 마지막 자리에 1을 더해줌
ex) 10101010 -> 01010110
보수의 뺄셈
: 컴퓨터는 감수를 1의 보수나 2의 보수를 취하여 피감수에다 덧셈함
* 1의 보수에서 오버플로에 의한 연산 처리가 복잡한 것은 캐리가 발생하면 최하위 비트에 1을 더해서이며, 2의 보수에서는 끝자리 캐리가 있으면 그것을 무시하므로 간단해 짐
1) 1의 보수의 뺄셈
- 피감수 M에 감수 N의 1의 보수를 취하여 덧셈
|
- 끝자리 올림 수(end carry)가 발생하면 최하위 비트에 1을 더함 - 끝자리 올림 수가 없으면 1의 보수를 취하여 덧셈하는 과정에서 얻은 결과를 다시 1의 보수를 취하고, 그 수 앞에 음수(-) 부호를 붙임 (Quiz6) 1의 보수를 이용하여 00001101(2)-00000110(2)를 하시오 ->00001101-00000110 ->00001101+11111001=1 00000110(캐리발생) ->00000110+00000001(캐리가 발생했기 때문에 최하위 비트에 1을 더함) ->00000111
(Quiz7) 1의 보수를 이용하여 00000110(2)-00001101(2)를 하시오 ->00000110-00001101 ->00000110+11110010=11111000(캐리가 발생하지 않음) ->-00000111(캐리가 발생했기 않았기 때문에 다시 1의 보수를 취하여 앞에 음수 부호를 붙임) |
2) 2의 보수의 뺄셈
- 피감수 M에 감수 N의 2의 보수를 취하여 덧셈
|
- 끝자리 올림 수가 있으면 그것을 무시 - 끝자리 올림 수가 없으면 2의 보수를 취하여 덧셈하는 과정에서 얻은 결과를 다시 2의 보수를 취하고, 그 수 앞에 음수(-) 부호를 붙임 (Quiz8) 2의 보수를 이용하여 00001101(2)-00000110(2)을 하시오 ->00001101-00000110 ->00001101+11111010= 1 00000111(캐리발생) ->00000111(캐리무시) |
2진수의 곱셈
: 2진수의 곱셈에는 여러 가지 방법이 있으나 일반적으로 곱셈의 원리는 반복적인 덧셈이므로 곱하는 수의 최하위 수를 조사하여 덧셈과 자리 옮김으로써 곱셈이 이루어짐
|
ex) 00110*0101 |
2진수의 나눗셈
: 2진수의 나눗셈은 나누어지는 수의 맨 윗자리와 나누는 수의 맨 윗자리를 맞춘 후 뺄셈과 자리 옮김으로써 나눗셈이 가능함
|
ex) 1110/11 |
* 컴퓨터에서의 2진 연산은 뺄셈, 곱셈, 나눗셈 모두가 덧셈으로 변환이 가능하기 때문에 컴퓨터 내부에서는 가산기(adder)를 이용하여 4식 연산을 수행한다
컴퓨터 내부에서의 데이터의 표현
컴퓨터 내에서 표현할 수 있는 문자: 영문자와 숫자, 특수기호, 한글 등의 여러 가지가 있으며 이들 문자는 2진수로 기호화(code)되어 기억장치에 비트단위의 조합으로 표현
비트(bit), 바이트(byte), MSB(Most Significant Bit)와 LSB(Least Significant Bit)
수치 데이터
: 사칙 연산의 대상이 되는 데이터를 말하는 것으로 정수(고정 소수점) 데이터 형식과 실수(부동 소수점) 데이터 형식, 10진 데이터 형식이 있음
2진화 10진 코드(BCD, Binary Coded Decimal)
: BCD 코드는 원래 10진수의 숫자를 나타내기 위해 4비트의 조합으로 만들었으나 영문자, 특수 문자 등을 나타내기 위해 그 비트를 추가한 6비트로 구성
: 10진법의 모든 수를 2진법의 8, 4, 2, 1의 4자리에 맞추어 표현하는 방법
: 6비트 BCD코드의 경우 표현 가능한 문자의 수는 2^6=64가지가 됨
- 존 비트(zone bit): 2진화 10진 코드 왼쪽의 2비트로서 전화 번호의 국 번호와 같은 역할을 함
- 디지트 비트(digit bit): 나머지 4비트로서 일련 번호와 같은 역할을 함
- 패리티 비트(parity bit): 기계적인 에러를 검사하는 용도로 사용하며 왼쪽 끝에 더 붙일 수 있음
|
|
ASCII 코드
: 7개의 비트로 구성된 코드이며 3개의 존(zone)과 4개의 숫자(digit)로 구성
: 앞 부분의 4개 부분 코드는 영문자, 특수 문자 등을 구분할 수 있도록 함
: 최근 패리티 비트를 추가하여 8자리의 2진 코드를 많이 사용함
*패리티 비트: 모든 비트열에 있는 1의 합이 항상 짝수 또는 홀수 개를 유지할 수 있도록 비트열에 추가한 검사 비트
: PC 기종에서 널리 사용되며 데이터 통신용으로 많이 사용됨
|
|
EBCDIC 코드
: 8비트로 구성된 코드이며 4개의 존(zone)비트와 숫자(digit)비트로 구성됨
: 8비트 코드이므로 2^8(=256)개의 서로 다른 문자를 표현
: IBM 대형 컴퓨터에서 기본으로 사용되었음
|
|
패리티 비트(Parity bit)
: 원래의 코드에 1비트의 검사용 비트를 덧붙여서 기계적 에러를 검사하기 위한 것이며 자기 테이프나 자기 디스크 등에서는 데이터 비트와 함께 기록
: 한 코드 내에서 자신을 포함한 전체 비트 중 1의 비트가 홀수개 또는 짝수개를 유지하게 함
|
|
해밍 코드(Hamming code)
: 해밍이 고안했으며 잘못된 정보를 발견하고 수정할 수 있게 한 코드
: 검사 비트가 최소 3개는 되어야 함
* 2진화 10진수의 4비트를 검사할 때에도 전체 비트가 4개이어야 함
* 검사용 비트위치는 1, 2, 4행에 패리티 검사 비트가 배열되고 3, 4, 6, 7행에는 디지트 비트가 배열됨
|
|
그레이 코드(Gray code)
: 비가중치 코드이며 연산에는 부적합하지만 어떤 코드로부터 그 다음의 코드로 증가하는 데는 하나의 비트만 바꾸면 됨
: 데이터의 전송, 입출력장치, 아날로그-디지털 변환기와 주변장치에 많이 사용됨
|
그레이 코드->BCD, BCD->그레이 코드 변환할때는 XOR연산을 사용함 |
액세스-3 코드(Excess-3 code)
: 8421코드에 3을 더한 코드로 3초과 코드 또는 3중 코드라고 함(8421코드보다 3이 더 큼)
: 자기보수 코드(self-complement cod)라고도 하는데 Excess-3 code의 0과 9, 1과 8, 2와 7 등이 1의 보수 관계에 있기 때문
: 이와 같이 자릿수가 특별한 의미를 지니지 않는 코드를 비가중치 코드라 함
: Excess-3 코드와 BCD 코드- BCD코드로 표현된 값에 3을 더하여 나타낸 코드이다
2-5진(biquinary) 코드
: bi는 2를 의미하고 quinary는 5를 의미하기 때문에 2-5진 코드라 한다
: 7개의 비트로 되어 있는데 그 비트 중에서 1의 개수는 두 개로 되어 있다
: 위치가 나타내는 값에 의해 가중치를 가지며 각 비트 순서대로 5043210의 의미를 가지므로 5043210코드라고도 함
|
|
링 카운터 코드(Ring counter code)
: 이해하기가 매우 쉬울 뿐 아니라 전자 회로를 사용하여 해독하는 것도 매우 용이함
: 각 코드 내에 1을 가지는 비트는 단 1개
: 이 코드에서 10진수로 변환시킬 경우 오른쪽 끝자리부터 왼쪽으로 오면서 가중치를 0, 1, 2, ..., 9로 주어 1비트의 값을 구하면 됨
|
|
2421코드
: 10진수를 2진수로 표현할 때 각 자릿수의 가중치가 2, 4, 2, 1
: 1111은 십진수 2+4+2+1을 더한 9가 됨
|
|
코드의 분류표
|
분류 |
코드종류 |
|
가중치 코드 |
BCD(8421), 84-2-1, Ring-Counter 등 |
|
비 가중치 코드 |
3초과(Excess-3), Gray, 2-out-of-5 등 |
|
자기 보수 코드 |
3초과(Excess-3), 2421, 51111, 84-2-1 |
|
오류 검출용 코드 |
해밍코드, 패리티 코드, 2-out-of-5 등 |
'삶의 늪에 들어 가기 전 > 정리중(미정리)' 카테고리의 다른 글
| [설계패턴]시스템 분석 설계 소개 정리 (0) | 2015.10.10 |
|---|---|
| [컴퓨터구조]명령어와 번지지정 방식 / 프로세서와 연산장치 정리 (0) | 2015.10.10 |
| [컴퓨터구조]시스템 성능측정 정리 (0) | 2015.10.09 |
| [컴퓨터구조]조합 논리회로 정리 (0) | 2015.10.09 |
| [컴퓨터구조]디지털 논리회로 정리 (0) | 2015.10.09 |

















